2022 SUSCTF
large case
1 | from Crypto.Util.number import * |
根据题目,e是p-1,q-1,r-1的一个因子之积

分解一下,考虑到最后一步肯定是开根然后CRT,e不可能太大,出题人也没那么好心,不会给你太小
所以ep应该是 757 或者 1709,eq 应该是66553,er应该是5156273
最后测出来 e = 757 * 66553 * 5156273
那么就先在 p , q , r 下分别进行一个 c 的“部分”解密,得出 m^ 757 % p, m^66553 % q,m^5156273 % r
考虑到这个 r 这部分实在是太大了,最后CRT的复杂度会很高。又注意到 原始 message的大小是介于 L 和 2L 之间的。最后是用 0 去填充到 3L 的。所以要想办法去掉这个填充。然后在 p 和 q 下去解 message 就可以了。去掉填充也很方便。因为是单纯的用 0 去填充的。所以相当于 m 乘以了一个 2^(8 * length),到 c 这里就是乘上了 2^(8 * length * e),所以最开始把 c 的这部分求逆求掉就好了。
然后就是在 p 下和 q 下 开根,再 CRT 结合。这一部分老生常谈,就不赘述了。
1 | import random |
InverseProlem
1 | import numpy as np |
代码很短啊,就是生成了一个矩阵,然后右乘了一下flag,给了输出。
原本以为给矩阵求逆一下就可以了,后来发现这个矩阵有点问题的,当 n 等于85 的时候,发现这个矩阵的行列式,,不能说是没有,也许是非常小叭。
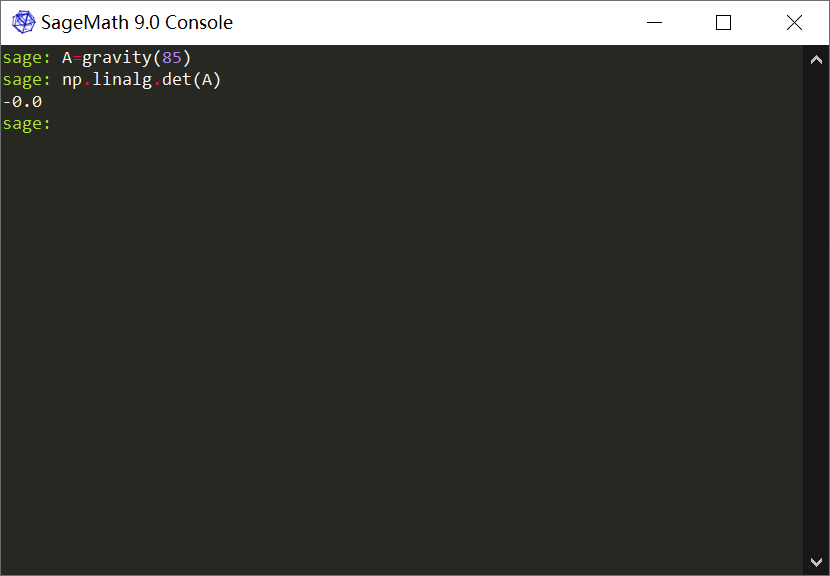
反正此时 A^-1 * A ! = E,所以直接求逆是不可能的。这里用的也是浮点数,所以直接解方程也是会出现精度问题,导致结果向量 b 好像加了噪声似的。唉,噪声?LWE啊,用格子去约。由于太小了。我这里我给他们都放大了一定倍数。为了把 b 里面的小数点给去掉,数了下大概要 16 个0。
然后全部取整,搞成int,再在 A 里面求一个 b 的CVP,然后直接右除拿到结果。
1 | import numpy as np |
Ez_Pager_Tiper
magic_box.py
1 | class lfsr(): |
problem
1 | from magic_box import * |
两个problem,三个lfsr伪随机数生成器,prob1用了lfsr1 和 lfsr2,magic是 1 << r,看到generator,对于两个lfsr的输出是放进了confusion,然后output = magic ^ c1 ^ c2,然后是while magic的循环, now, magic = self.malicious_magic(magic),经过测试,当 magic 等于 1 << r 的时候,也就是 2 的幂次的时候,
(-magic & magic) = magic,所以 now = magic, magic = 0,循环只会走一趟。接下来now取最高位,肯定是 1了,output异或一下now,相当于异或magic,那就只剩 c1 ^ c2 了。出来后 output ^= cnt * c1,cnt此时是1,所以output最后只剩 c2 了。所以 output = input ^ c2
1 | def malicious_magic(self, magic): |
那么,看到题目另一个data文件夹里,发现文件都是以Date: 开头的,然后lfsr2又只有12级,所以爆!也就是 4095^2
爆了之后就知道seed2和mask2了。
然后看到prob2,此时给出magic是一个素数,同样经过测试,会发现,所有的循环走完后,cnt是0,异或now的部分叠加起来,最后就是magic。所以最后的输出 output = input ^ c1 ^ c2
注意到,文件都是以Date: 开头,解密第一个prob也获得了线索,就是Date: 后面的日期就是文件名解base64,所以最后搞出来我们能获得16字节明文。有了16字节的明文、密文,然后这里我们是知道mask2的,我们只需要爆4095个seed3就能获得4095个c2,从而得到4095个16字节的c1。注意到lfsr1是64级的,那么我们只需要64 * 2 = 128 bit = 16 字节的输出就能恢复lfsr的所有参数了。所以我们用4095个c2去恢复参数,然后生成相应的密钥流,尝试解密,观察结果。
1 | from Crypto.Util.number import * |
SpecialCurve3
1 | from Crypto.Util.number import * |
三个problem,有几个华点,生成prime的方式没给,估计有蹊跷。果不其然,经过全都是p+1 smooth的。所以三条线中阶要是等于p+1,就能直接爆了。
第二个华点,problem1用的p很小,显然是要把曲线上的点映射到整数域上去开log。
第三个华点,problem2的 a = 0,一般来说是条奇异曲线,可能会有些比较简单的映射规则。(那么第一个华点应该是给problem3用的了)
先看第一个,不难看出是条圆锥曲线:y^2 = a x ^ 2 + b x
此时 a 是一个二次剩余,我们记为 y^2 = a^2 x ^ 2 + b x 好了。

用共点推的,然后直接测这个映射
f: (x,y) -> (k+a)/ (k-a)
e · (x,y) -> ((k+a)/ (k-a) )^e 其中k = y / x
发现不是共点的时候也满足,那么第一个problem解决。
第二个problem,a = 0,从上面看就知道 k2 = k1 / 2,所以y2 = y1 * x2 / (2 * x1),把 x 都用 y 表示一下,消一下,就得到了 2 * y1 = y2,再简单测一下就能发现是一个简单的倍数关系,那除一下就好了。
第三个problem,此时给 a 取负了,那么这一部分就不是二次剩余了,有限整数域下我们是求不出上面的 a 的(就是开根),所以估计要用到第一个华点,测一下这条线的阶,乘一下p +1 发现回到 0 了,那么显然了,这里就去子群里爆破求解,最后crt组合得解。
去子群里爆破的步骤,就是把G 和 Q 都降阶(就是两边乘以 (p + 1) // order),此时G 和 Q 的阶都是 order 了,然后就在这个order里去爆,当 i * G == Q 时,此时 i = e % order,
1 | from Crypto.Util.number import * |
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081,也可以邮件至 643713081@qq.com
文章标题:2022 SUSCTF
文章字数:3.7k
本文作者:Van1sh
发布时间:2022-02-28, 11:18:35
最后更新:2022-02-28, 20:50:10
原始链接:http://jayxv.github.io/2022/02/28/2022 SUSCTF/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

